Метод конечных элементов для решения задач в области физики

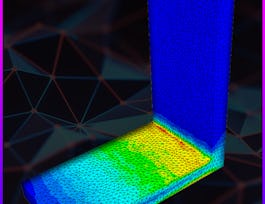
This course is an introduction to the finite element method as applicable to a range of problems in physics and engineering sciences. The treatment is mathematical, but only for the purpose of clarifying the formulation. The emphasis is on coding up the formulations in a modern, open-source environment that can be expanded to other applications, subsequently. The course includes about 45 hours of lectures covering the material I normally teach in an introductory graduate class at University of Michigan. The treatment is mathematical, which is natural for a topic whose roots lie deep in functional analysis and variational calculus. It is not formal, however, because the main goal of these lectures is to turn the viewer into a competent developer of finite element code. We do spend time in rudimentary functional analysis, and variational calculus, but this is only to highlight the mathematical basis for the methods, which in turn explains why they work so well. Much of the success of the Finite Element Method as a computational framework lies in the rigor of its mathematical foundation, and this needs to be appreciated, even if only in the elementary manner presented here. A background in PDEs and, more importantly, linear algebra, is assumed, although the viewer will find that we develop all the relevant ideas that are needed. The development itself focuses on the classical forms of partial differential equations (PDEs): elliptic, parabolic and hyperbolic. At each stage, however, we make numerous connections to the physical phenomena represented by the PDEs. For clarity we begin with elliptic PDEs in one dimension (linearized elasticity, steady state heat conduction and mass diffusion). We then move on to three dimensional elliptic PDEs in scalar unknowns (heat conduction and mass diffusion), before ending the treatment of elliptic PDEs with three dimensional problems in vector unknowns (linearized elasticity). Parabolic PDEs in three dimensions come next (unsteady heat conduction and mass diffusion), and the lectures end with hyperbolic PDEs in three dimensions (linear elastodynamics). Interspersed among the lectures are responses to questions that arose from a small group of graduate students and post-doctoral scholars who followed the lectures live. At suitable points in the lectures, we interrupt the mathematical development to lay out the code framework, which is entirely open source, and C++ based. Books: There are many books on finite element methods. This class does not have a required textbook. However, we do recommend the following books for more detailed and broader treatments than can be provided in any form of class: The Finite Element Method: Linear Static and Dynamic Finite Element Analysis, T.J.R. Hughes, Dover Publications, 2000. The Finite Element Method: Its Basis and Fundamentals, O.C. Zienkiewicz, R.L. Taylor and J.Z. Zhu, Butterworth-Heinemann, 2005. A First Course in Finite Elements, J. Fish and T. Belytschko, Wiley, 2007. Resources: You can download the deal.ii library at dealii.org. The lectures include coding tutorials where we list other resources that you can use if you are unable to install deal.ii on your own computer. You will need cmake to run deal.ii. It is available at cmake.org.